
Activity vs. Inquiry – Which Truly Promotes Cognitive Rigor?
One of the most helpful tools we educators can use to determine the cognitive rigor of learning experiences is the Cognitive Rigor Matrix or Hess Matrix developed by Karin Hess, Dennis Carlock, Ben Jones, and John Walkup. This matrix aligns the level of thinking students are expected to demonstrate and the depth of knowledge required to answer questions, address problems, accomplish tasks, and analyze texts and topics.
This graphic is the version of the matrix published in one of Hess, Carlock, Jones, and Walkup’s white papers (2009). The matrix is intended to be used as a resource and tool for teachers to categorize activities and inquiries based upon their level of complexity.
However, what truly defines and drives the cognitive rigor of a learning experience – the activity or the inquiry?
We can present our students with dozens of questions to answer, problems to address, tasks to accomplish, and texts and topics to analyze. We can provide learning experiences that engage students in discussion, experimentation, analysis, and evaluation of ideas and information. We can also provide students opportunities to develop and demonstrate their talent and thinking by using what they have learned by designing, developing, and doing projects. We can have students role play, re-enact, or participate in simulations – both controlled and uncontrolled.
However, do those learning activities truly promote cognitive rigor?
Consider how math has historically been instructed and assessed. In the past, students proved they learned the mathematical concepts, operations, and procedures they were taught by solving a series of problems presented to them correctly. If they solved a problem correctly, then they prove they know how to do the math. The more problems students solve correctly, the more proof we have that the student knows how to do the math that was taught to them.
With cognitive rigor, knowing what are the mathematical facts and how can the mathematical concepts, operations, and procedures can be used to solve problems is half the battle. Students must know – or think strategically – how and why they can use the math they are learning to do the following:
- Reason abstractly as well as quantitatively by explaining the meaning of quantities, not just how to compute them (CCSS.MATH.PRACTICE.MP2)
- Justify their conclusions, communicate them to others, and respond to the arguments of others. attend to precision communicating precisely (CCSS.MATH.PRACTICE.MP3)
- Communicate precisely to others by using clear definitions in discussion with others and in their own reasoning, stating the meaning of the symbols they choose, and give carefully formulated explanations to each other. (CCSS.MATH.PRACTICE.MP6)
Look at the cognitive actions in these objectives: explain, justify, communicate, respond, state. These actions are not done or shown. They are expressed or told.
We can present students with a series of mathematical and word problems and requiring them show their work or tell why the answer is correct for each problem. However, cognitive rigor prompts and encourages students not only to express and share the depth and extent of their learning but also to think deeply about how and why they can transfer and use what they have learned
That’s accomplished by challenging students to show and tell the following:
- What is the knowledge?
- How can the knowledge be used?
- Why can the knowledge be used?
- What else can be done with the knowledge?
- What can you do with the knowledge?
The inquiry prompts students to think about what they are learning and encourages them to express and share what they have learned in detail, insightfully, and in their own unique way. The complexity is determined not just by the question but also how deeply or extensively the student responds to the question. Consider a 6th grade math unit on the number system. By the end of the unit, the student will be able to compute fluently with multi-digit numbers and find common factors and multiples. That’s the academic goal for the unit. As part of the unit, students will fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation (CCSS.MATH.CONTENT.6.NS.B.3). That’s the educational objective. Students are presented these mathematical problems to demonstrate they can fluently multiply multi-digit decimals using the standard algorithm for addition and multiplication.
Cognitive rigor teaches students to think – not what to think or how to think but think deeply about the texts and topics they are learning. When they are first introduced with a word or term they don’t understand or never heard of before, they should ask what does it mean. When they are first introduced to an idea, subject, or topic, they should inquire who, what, where, or when. When they are presented with a scenario or situation, they should inquire how or why and investigate what is the cause, the connection, or the consequence. Once they have developed the factual, conceptual, and procedural knowledge, they should be encouraged to think creatively about what if or think critically about choices, conclusions, and decisions. Most importantly, they should be encouraged to express what do you believe, think, or feel; share what can you design, develop, or do; or show how could you or how would you answer a question, address a problem, accomplish a task, or analyze a text or topic.
Of course, students need to be presented and provided with an activity which will prompt them to ask and address these questions. However, should the emphasis be on completing the activity or responding to the inquiry?
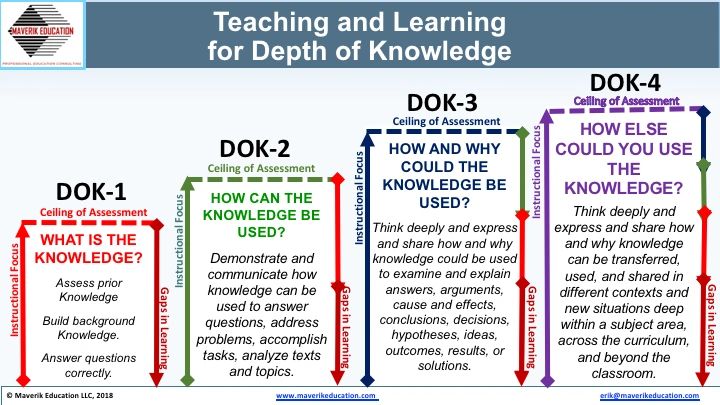
There’s one more action cognitive rigor expects students to do – communicate. That’s where depth of knowledge comes into play. Depth of knowledge establishes the context in which students are to demonstrate and communicate their learning. A learning experience at a DOK-1 level focuses primarily on knowledge acquisition – demonstrating and communicating what is the knowledge A learning experience at a DOK-2 level targets knowledge application – demonstrating and communicating how can the knowledge be used to answer questions, address problems, accomplish tasks, and analyze texts and topics. A learning experience at a DOK-3 level engages students in knowledge analysis – demonstrating and communicating why can the knowledge be used attain and explain answers, conclusions, decisions, outcomes, results, and solutions. A learning experience at a DOK-4 fosters and promotes knowledge augmentation – demonstrating and communicating what else can be done with the knowledge, how else can the knowledge be used in different contexts, and – most importantly – what can you design, develop, and do with the knowledge?
The activity, therefore, can be used to establish the context in which students are to express and share their depth of knowledge. However, cognitive rigor also expects students to think – hence why it’s called cognitive rigor. Thinking is prompted and promoted by inquiry and questioning. It stimulates deeper thinking by prompting students to consider, contemplate, or critique. It extends thinking by promoting students to think critically, creatively, and strategically.
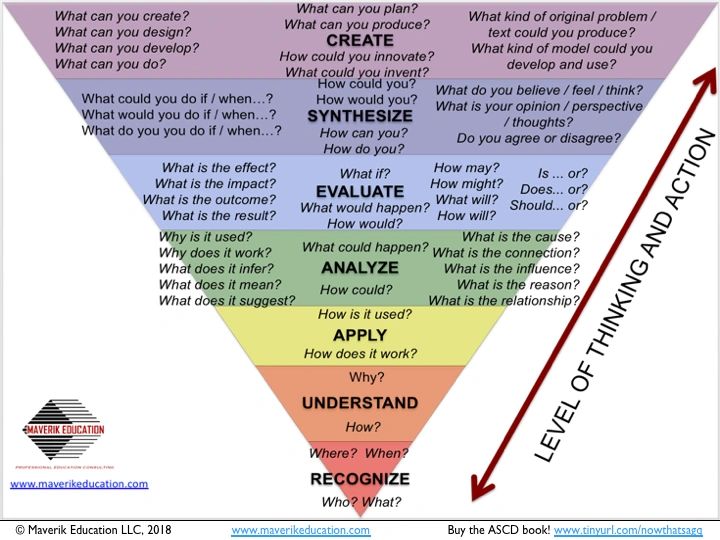
Most importantly, inquiry promotes flexibility in thinking. With educational objectives, students are expected to demonstrate whatever that cognitive verb that academic standard or performance objective states. These are generally the verbs associated with the cognitive process dimension categorized in Bloom’s Revised Taxonomy – remember, understand, apply, analyze, evaluate, create. Inquiry not only promotes deeper thinking but also increases the cognitive complexity of learning experiences. Asking how or why can challenge students to understand, apply, analyze, or evaluate. Referring to you in the inquiry shifts the instructional focus from demonstrating and communicating conceptual and procedural knowledge to expressing and sharing self-knowledge and personal understanding. Hypothetical questions encourage students to develop conditional and contextual knowledge as well as think critically and creatively about possibilities, practicality, and potential. Argumentative questions promote thinking at the deepest levels – specifically, decision-making and problem solving that involves understanding, analyzing, evaluating, synthesizing, and creating. That’s teaching and learning for cognitive rigor, and that’s what a good question promotes.
If you’re teaching for compliance – can students apply a concept or procedure to answer a question, address a problem, accomplish a task, or analyze a text or topic correctly – then student learning should focus primarily on the activity. If you’re teaching for cognition – or to promote cognitive rigor by having students think deeply and express and share the depth and extent of their learning – then ask a good question that will set the instructional focus and serve as the assessment for student learning. Have the activity serve as the textual evidence or example that will support the students’ response to the good question.

Erik M. Francis, M.Ed., M.S. is an author, educator, and speaker who specializes in teaching and learning that promotes cognitive rigor and college and career readiness. He is also the author of Now THAT’S a Good Question! How to Promote Cognitive Rigor Through Classroom Questioning published by ASCD. He is also the owner of Maverik Education LLC, providing academic professional development and consultation to K-12 schools, colleges, and universities on developing learning environments and delivering educational experiences that challenge students to demonstrate higher order thinking and communicate depth of knowledge.
